
编辑:杜伟、陈萍算法的改进到底能带来多大的益处?来自 MIT 的研究者撰写了有史以来第一次对算法进展研究的综合分析论文。在综合研究后,他们发现对于大型计算问题,43% 的算法改进等于或大于摩尔定律带来的益处;在 14% 的问题中,算法对性能的改进大大超过了硬件改进带来的益处。

算法决定了计算机使用哪种计算方法来解决问题,是计算机科学的核心支柱之一。随着算法的改进,研究人员可以探索更难的问题并开创新的领域和技术。对于算法的发展速度,人们已经做出了大胆的断言。例如 PCAST(一个为美国总统提供建议的资深科学家团体)曾在 2010 年写道,在许多领域,由于算法的改进所带来的性能提升,远远超过了由于处理器速度的提高所带来的显著性能提升。然而,这一结论是基于线性求解器的进展数据支持的,这只是一个单一例子。一般来说,由于不能保证线性求解器代表算法,因此我们不清楚应该对 PCAST 等结论进行多大范围的解释。
关于算法与计算机的关系,有人说算法有点像计算机的父母。它们告诉计算机如何理解信息,反过来,算法又可以从计算机中获得有用的东西。算法效率越高,计算机要做的工作就越少。对于计算机硬件的技术改进,以及备受争议的摩尔定律是否到达极限,其实,计算机性能只是问题的一方面。另外,算法也在不断的改进,相应的,所需的计算能力变得更少。虽然算法效率问题可能不太受到太多关注,但你肯定会注意到这种情况,搜索引擎突然变快。
来自 MIT 计算机科学与人工智能实验室 (CSAIL) 的科学家提出疑问:算法改进的速度到底有多快?
为此,他们撰写了有史以来第一次对算法进展研究的综合分析,文章题目为《 How Fast Do Algorithms Improve? 》,并发表在 IEEE Proceedings 上。

论文链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9540991
这项研究使我们能够系统地查看算法是何时被发现的,它们是如何被改进的,以及算法改进的规模与其他创新研究相比结果如何。本文分析了来自 57 部教科书和超过 1137 篇研究论文,以追溯算法何时变得更优。其中一些研究论文直接报告了新算法带来的好处,而其他研究论文需要使用伪代码(描述基本细节算法的速记版本)进行重构。
该团队总共研究了 113 个算法族, 对于每个算法,该团队都重建了它的历史,跟踪每次针对该问题所提出的新算法,并特别强调那些更有效的算法。从 1940 年代到现在,从性能上看,该团队发现每个算法族平均有 8 个算法,其中有几个提高了效率。为了共享这个知识数据库,该团队还创建了 Algorithm-Wiki.org。
此外,该研究还绘制了这些算法族改进的速度,他们重点关注那些算法中经常被用来分析的特征,这些特征能保证以最快的速度解决问题。
对于大型计算问题,43% 的算法改进等于或大于摩尔定律带来的益处。在 14% 的问题中,算法对性能的改进大大超过了硬件改进带来的益处。对于大数据问题,算法改进带来的益处也非常大,因此算法改进的重要性在近几十年来不断增加。
Neil Thompson 与麻省理工学院访问学生 Yash Sherry 一起撰写了这篇论文。其中 Thompson 是麻省理工学院计算机科学和人工智能实验室研究科学家,也是哈佛大学创新科学实验室的客座教授。他的主要研究领域包括摩尔定律与计算机性能、机器学习与算法等。

Neil Thompson
分析结果
在分析中,研究者着重于具有精确解的精确算法。他们将算法分类为解决不同潜在问题的算法族。例如,合并排序和冒泡排序是比较式排序族中 18 种算法中的两种。最终,基于一系列标准,研究者共探究了 113 个算法族。
平均而言,每个族有 8 种算法。如果一种算法降低了其算法族的最坏情况渐进时间复杂度,则认为它改进了。基于这一标准,研究中得到了 276 种初始算法和后续改进算法,其中每个算法族中初始算法平均会有 1.44 个改进。
创建新算法
下图 1 总结了随时间推移出现的算法发现和改进。其中,1(a) 展示了每个算法族中首个算法出现的时间,通常通过蛮力实现(意味着直接但计算效率低下),1(b) 展示了每十年中算法的份额,其中渐进时间复杂度提升。
例如,20 世纪 70 年代发现了 23 个新的算法族,并对先前发现的所有算法族中的 34% 进行了改进。以后数十年,发现和改进的速度下降了,表明这些算法的进展放缓了。尚不清楚究竟是哪些原因造成的,一种可能的原因是某些算法在理论上已经达到了最优,因此不可能取得进一步发展。
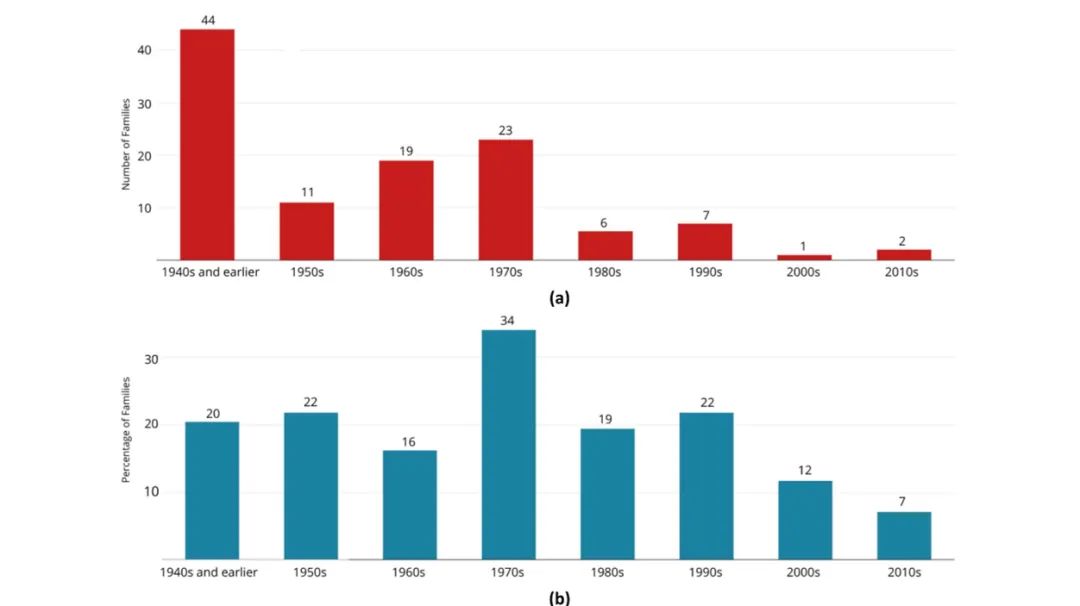
下图 1 (c) 和 1(d) 分别展示了算法首次被发现时的「时间复杂度类别」分布以及因算法改进使得一类算法转变为另一类的概率。在算法理论中,时间复杂度类别根据算法本身需要的操作数量(通常表示为输入大小函数)进行分类。
如 1(c) 所示,在被发现时,31% 的算法族属于指数复杂度类别(表示为 n!|c^n )。这意味着随着输入大小的增长,算法至少会进行指数级的运算。1(d) 则表明,随着算法设计者发现更高效的实现方式,算法的复杂度类别会出现重大的转变。
衡量算法改进
随着时间推移,算法族的性能会随着「用更少操作解决相同问题的新算法的出现」而提升。为了衡量进展,研究者着重于提升渐进复杂度的发现,例如从 O(n^2) 到 O(n log n) 或者从 O(n^2.9) 到 O(n^2.8)。
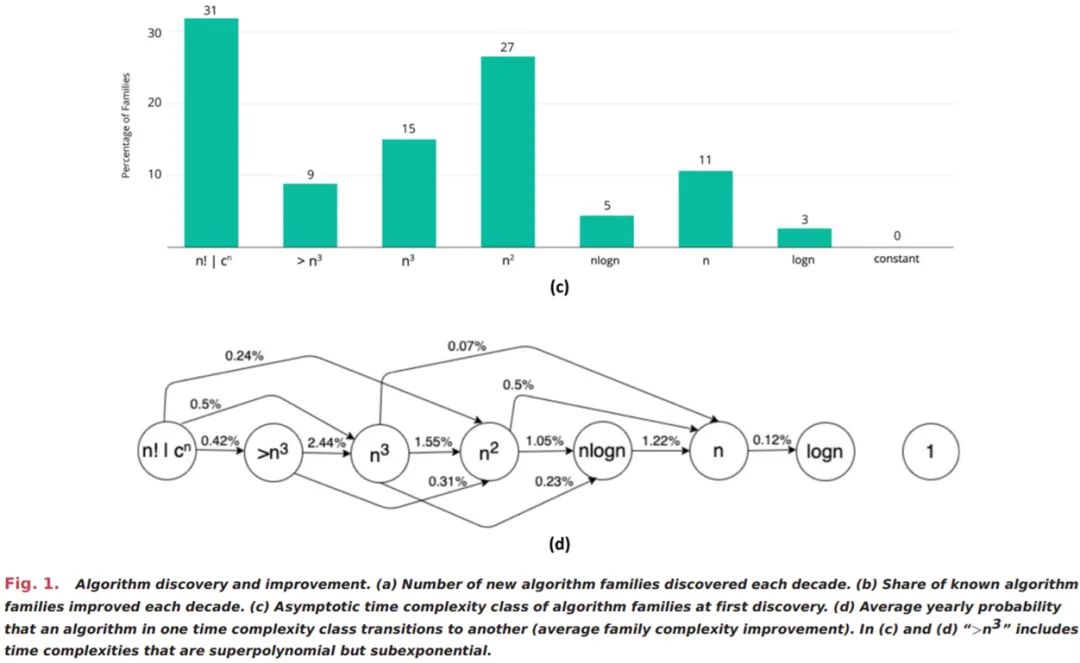
下图 2 (a) 展示了四个不同算法族(不同颜色表示)随时间推移出现的进展。对于每个算法族,首个算法的性能都被归一化为 1。每当发现一种算法具有更高的渐进复杂度时,则由垂直步进(vertical step up)表示。比如,对于 n = 100 万的问题规模而言,最大子串等算法的改进速度明显快于硬件或摩尔定律,而自平衡树创建等其他算法不呈现这种特点。
算法和硬件改进之间的重要对比在于改进的可预测性。虽然摩尔定律使得硬件随时间推移顺利地改进,图 2 展示了那些经历了大的但不频繁的改进的算法。
此外,一种算法的渐进性能关乎于问题输入大小的函数。随着输入的增加,从一个复杂度类别转变到另一个复杂度类别的改进的规模也在增加。图 2(b) 展示了「最近邻搜索」族的这种效果,表明当输入大小从 10^2 增加至 10^8 时,改进大小也从 15 倍增至约 400 万倍。
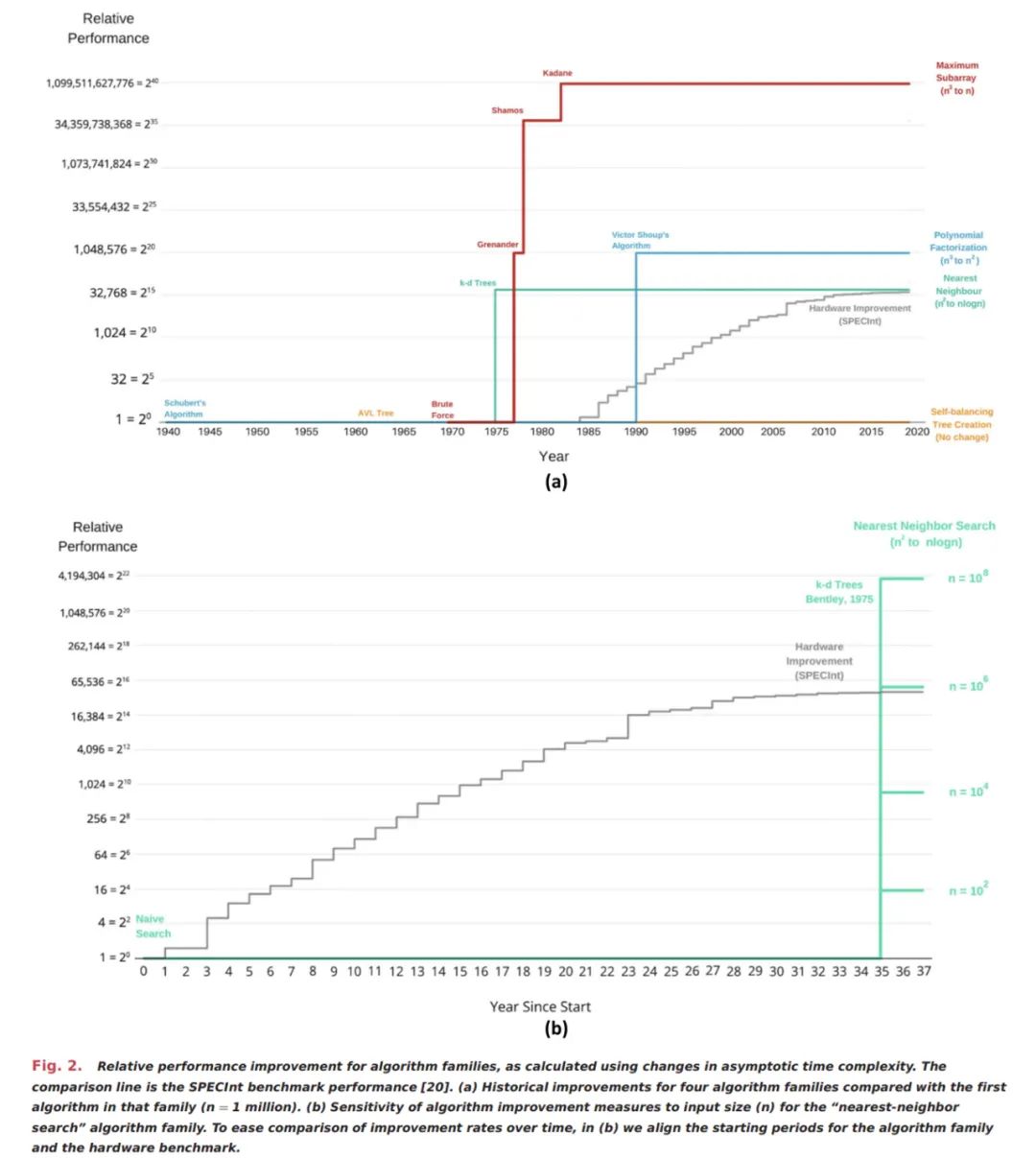
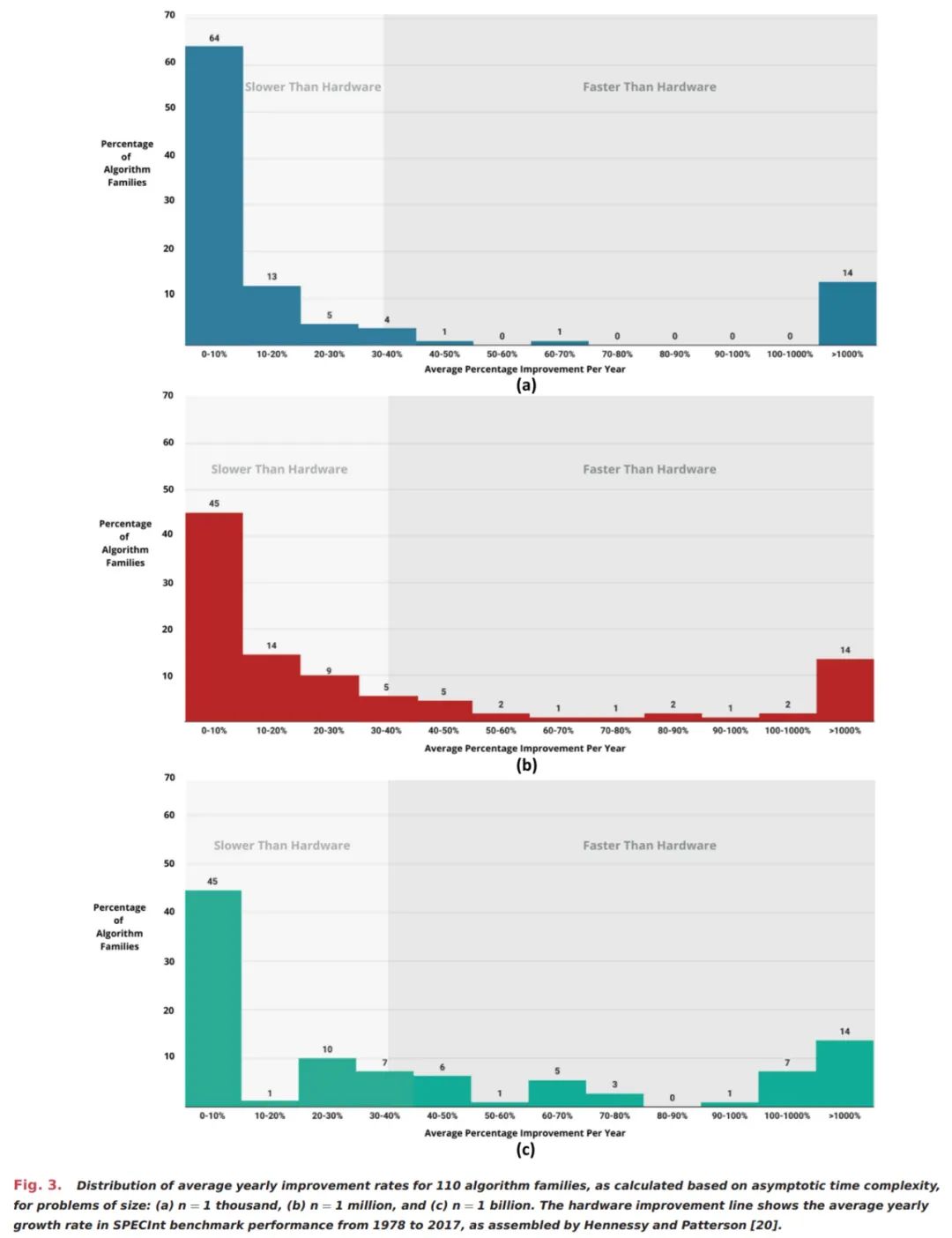
上图 2 展示了算法改进对四个算法族的影响,下图 3 将这种分析扩展至了 110 个算法族。具体地,研究者展示了问题规模分别为 1 千、100 百万和 10 亿时平均年度改进率,并将它们与 SPECInt 基准衡量的硬件平均改进率进行比较。
如下图所示,研究者展示了两种大的算法族集群,以及一些中间值。
第一个集群代表不到一半的算法族,即使对于大的问题规模而言,它们几乎没有出现改进。这个集群可能包含那些获得很少关注的算法族、在数学上已经达到最优实现并因而无法进一步改进的算法族、那些仍然无法解决某种大小的问题的算法族或者其他。
第二个集群包含 14% 的算法族,它们的年改进率超过 1000%。这些算法受益于指数级加速,例如当初始算法具有指数级时间复杂度时,后续的改进使得问题可以在多项式时间内解决。
研究者的结果量化了算法改进影响计算机科学的两个重要教训。
其一,当一个算法族从指数级复杂度过渡到多项式复杂度时,它会以一种硬件改进无法做到的方式转变该问题的易处理性;
其二,随着问题规模增加至数十亿或万亿个数据点时,就平均年改进率而言,算法改进的重要性比硬件或摩尔定律重要得多。这些发现表明,在拥有大规模数据集的数据分析和机器学习领域,算法改进尤为重要。
算法中的 Step 分析
在整篇文章中,该研究通过查看算法的渐进复杂度来估算算法需要执行的 step 数。
为了估计渐近复杂度近似的保真度,该研究重新分析了算法改进的研究。由于数据库中只有 11% 的论文报告了算法所需的算法 step 数,因此研究者需要尽可能根据原始论文中的伪代码描述手动重建 step 数。
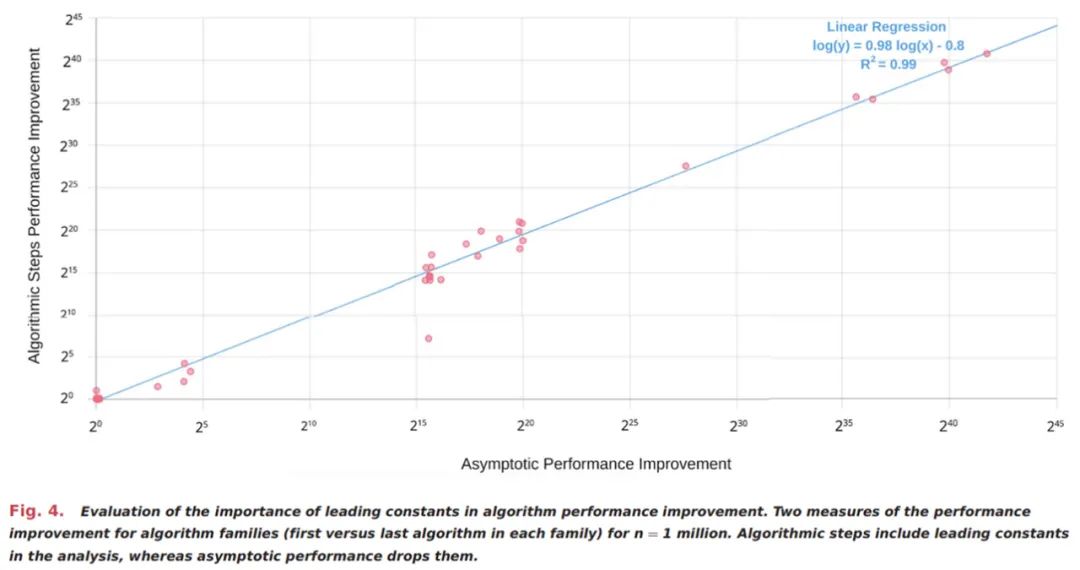
使用这种方法,该研究能够重建 65% 的算法族中第一个和最后一个算法所需的算法 step 数。图 4 显示了算法 step 改进和渐近复杂度改进之间的比较。
图 4 显示,在数据可用的情况下,算法 step 数和渐近性能的改进大小几乎相同。
参考链接:
https://news.mit.edu/2021/how-quickly-do-algorithms-improve-0920
https://ieeexplore.ieee.org/document/9540991